

Moments of inertia may be expressed in units of kilogram metre squared (kg The amount of torque needed to cause any given angular acceleration (the rate of change in angular velocity) is proportional to the moment of inertia of the body.
#Mass moment of inertia of a circle free
When a body is free to rotate around an axis, torque must be applied to change its angular momentum.
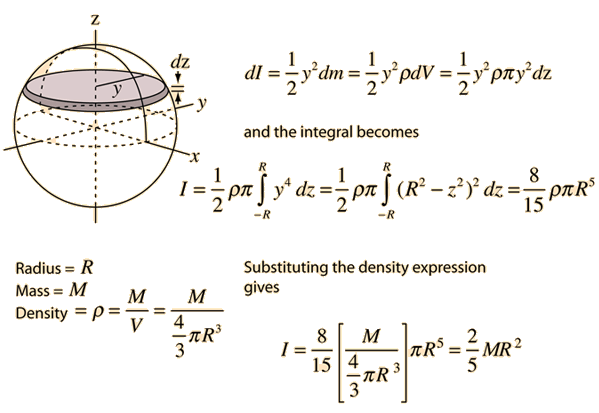
7.3 Derivation of the tensor components.7.2.1 Determine inertia convention (Principal axes method).6.5 Scalar moment of inertia in a plane.6 Motion in space of a rigid body, and the inertia matrix.For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3 × 3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other. Its simplest definition is the second moment of mass with respect to distance from an axis.įor bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation. The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. Here is how the Moment of inertia of rod about an axis through its center of mass and perpendicular to rod calculation can be explained with given input values -> 295.4167 = (35.45*(10^2))/12.War planes have lesser moment of inertia for maneuverability.
#Mass moment of inertia of a circle how to
How to calculate Moment of inertia of rod about an axis through its center of mass and perpendicular to rod using this online calculator? To use this online calculator for Moment of inertia of rod about an axis through its center of mass and perpendicular to rod, enter Mass (m) & Length of Rod (L) and hit the calculate button. Moment of Inertia is denoted by I symbol. Moment of inertia of rod about an axis through its center of mass and perpendicular to rod calculator uses moment_of_inertia = ( Mass*( Length of Rod^2))/12 to calculate the Moment of Inertia, Moment of inertia of rod about an axis through its center of mass and perpendicular to rod is a quantity expressing a body's tendency to resist angular acceleration, which is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation. How to Calculate Moment of inertia of rod about an axis through its center of mass and perpendicular to rod?


 0 kommentar(er)
0 kommentar(er)
